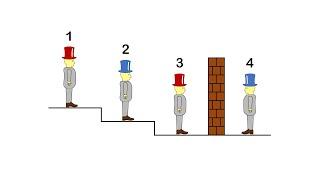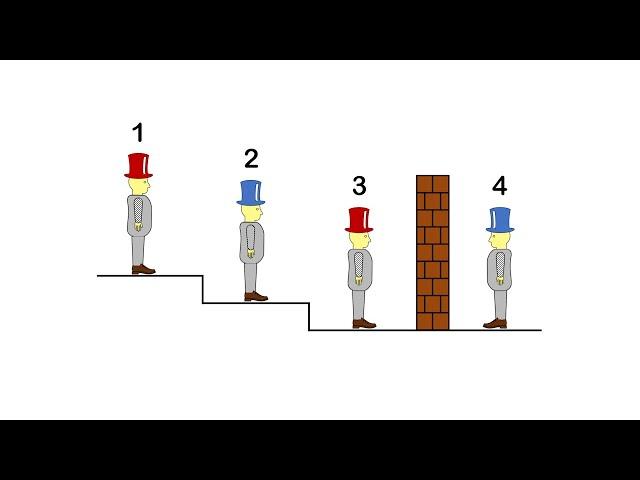
Can You Solve The 4 Hats Logic Puzzle?

i got this one right only because i know you leave important information out and i saw the Green-eye logic puzzle on another channel and its basically the same thing. i think you need to make clear who can see who. the first man can see BOTH men in front of him.

To break it down, the first magician can't see anything except his own hat. The second magician behind the wall cant see anything execpt his own hat. The third one can see the hat of the second one infront of him and can tell the hat of his and his own. The third one can see everything.

Now, the third locician makes a computation. Let R be red and blue be white:

RBRB BRRB
BRBR RBBR
BBRR BBRB
RRBB RRBR

He contemplates everything, since the third magician can see red and blue, he picked the option which had RB in it.

(Finish the answer)

I'm proud of myself for getting this but I only got it because I saw the original video and applied the same trick.

I didn't listen to the actual question properly and was sitting here cracking head trying to figure out which logician would know the colour of the hat of the logician being the wall. When I've solved this in about the first 3 mins 😂😂

if u ever feel useless , remember logician 4

Technically it doesn't matter what 1 says. We can't see 4 so he's out of the guessing game. If 1 says red then 2 knows his is blue as he sees 3's red hat. If 1 says he's blue and 2 only sees 3's red hat he can also say blue as then 3 can with certainty pick red as there are no other blue hats. So both of what 1 picks let's them all free

As a logical person, mathematicians drive me crazy. What does 4! over 2!2! even mean?

It's obvious that the 1st guy won't say anything because he sees 2 different coloured hats, so after a bit the 2nd guy works this out and knows he has a different hat to the guy in front of him, so says "Blue", then the 3rd guy hearing this knows he has a red hat. The 1st and 4th don't have a clue, but only 1 of them needs to get it, and 2 of them knew for certain.

what if logician 1 was mute or colourblind 😂

These things are better than wasting time on social media

Logicians 3&4: 👁️👄👁️

I can’t stand the fact that you think logicians can’t ALSO be criminals

If they can only look forward, how do any of them know how many people are behind them or ahead of them on the other side of the wall. They would really never know what position they were in.

sometimes, silence is a message

Can you j say if 2 and 3 wear same hat, 1 knows his and 4th hat is the other colour so one gets the answer correct, if 2 and 3 where different hats, 1 can guess any colour, if he gets it right then though the answer will not be counted as 1 wasn't sure, but 4 knows that if 1 isn't sure then 2 and 3 where diff. Hats so if 1 gets right answer 4 immediately knows that his hat is the opposite of 1's answer, if 1 gets it wrong, than 4 knows that 1's ans is the colour of his hat



So with assurity 4 can tell his colour even if the arrangement of these hats are different than shown

2 can know for sure

I would have just glanced up slightly at the rim of my own hat.

What got me on this one was that they weren't allowed to talk to each other. That threw me off, because the solution depends on person 2 realizing that person 1isn't able to answer. It makes sense after the fact, but lets just say it's a good thing I wasn't person 2. LOL

This was really easy bruh

3 and 4 has no information at all, they can't figure it out.
1 could have enough info. But doesn't speak, as he sees 2 different hats. If he'd see the same color twice, he'd know he's the opposite color.

That leaves us 2 who now knows he's part of a group of 2 different colors, and he knows one of those colors. Thus, he can state his own.

Simple answer is - 2nd person knows the color of hat of 3rd person so if color of hat of 2nd and 3rd person is same so one can answer easily. If they are different so 2nd person thinks that 1st person is not answering that means 2nd and third person have hats of different colors 😊

I kept wondering why you were pronoucing 'magician' in such a funny way

The way the puzzle is set up makes me think there exists no time dimension. Tricky!

It was the simplest one😊

I started thinking that every logician needed to guess which hat they had, but so i was stuck on a case where 2 and 3 knew their hats and 1 e 4 didnt, lol.

I was presented with this problem during an interview. I totally biffed the answer, but they still hired me!

I used to give this puzzle to my students only the hats were worn by all knowing witches on Halloween.

take the hat and see the color, not against the rule🤷🏻‍♂

What I did wrong was assuming that they couldn't hear their answers. I assumed that somehow they would give an answer without the others knowing they did so, I wouldn't have considered the 1st guy was confused and that confusion would influence the 2nd guys answer.

my guess is if 1 doesnt speak then 2 must know that he and the next person have a different colored hat and would say blue.

Easy puzzle, not even a logic, with a bit messy solution

So we're just going to ignore that no talking rule.

Logical people who are purely logical do not make time-based assumptions. Nice puzzle though

Jp here again, Thank you MindYourDecision :)

If they were given the hats by the warden, wouldn't they all already know the color?

We dont need to sort out cases ... if person 1 didnt answer imply ... person 2 know he has different hat than no 1 ... so he says opp of red as blue.

You didn't say that they could communicate... If 2 knows 1 is confused they communicated

A logical puzzle that doesn’t logically explain how 3 and 4 are innocent.

This is set up really poorly. You made out that they couldn't communicate. I took this to mean that they wouldn't know whether someone else had a correct answer or not, leading me to believe it was impossible.

The answer is a cheat. logician 2 only looks forward, so he wouldn't be able to know for sure that logician 1 is confused. And you said that logicians would only answer if they are 100% sure of their answer. But there can be many reasons why logician 1 is taking time to answer, so logician 2 isn't actually 100% sure.
My idea was that logician 1 would tell logician 4 to jump. Logicians are only allowed to look forward, but they are not forbidden to jump in place. This would give logician 1 the information they're missing.

i solved it as fallows: if 1 sees two reds or two blues he says I know my color, it is the opposite of the two i can see. otherwise 1 says I don't know. 2 knows that this means that one sees two colors of hats therefore 2 says his hat is the color not 3 so if 3 is blue 2 says red and if 3 is red 2 says blue.

And what is the significance of logician 4 facing the wall also😂😂😂

I would just assume, if I was number two, that I was wearing a blue hat because if it was a red hat like the person in front of me then the person behind me would see two of the same color hats in front of him and know right away what color hat he had

dude number 4 carried fr

Nice. Thanks for detailing the different possibilities.

I actually have this riddle in an old book, you cannot trick me today you wizard!

How can they guy in position 1 know hat colors 2 & 3 if everyone is exactly the same height and shape? person 3 would be 100% hidden from person 1. The height of all people is linear. The only way to solve this problem is if the stairs progressively get shorter and shorter as they progress to the bottom, like a logarithmic curve.

This one was very easy for me, because I started directly with Number 1's thinking.

Given that he saw blue red, he knew he had a 50% chance of guessing correctly. Only 2 hats remained that he and 4 could wear, one blue, one red. So he wasn't sure.

Then, 2 saw red.
2 knew 1 didn't know.

Since 2 saw red, 2 immediately knew that he can not be wearing red as well, otherwise 1 would have immediately said he was wearing blue.

Solved easily

This is quite easy if you think about it for a second, didn’t take me that long to figure out. You don’t have to do any of the math you did or think of all possible combinations. If you’re man #2, you know that man #1 will speak up if he sees 2 of the same color hats. If he doesn’t, he must be seeing 2 different color hats, meaning you as #2 are wearing the opposite color as the man in front of you. Same concept as you explained but without all the unnecessary steps

2 sees a red a hat. 1 doesn't know because he sees 1 blue and 1 red. This tells 2 that his hat must be blue, because if it was also red 1 would say his hat is blue.

Similar to the question: you're in a totally dark room with a drawer full of socks. ALL black and white. How many do you need to take to be sure you have a matching pair? Same logic, applied inversely.