How to Calculate Pi, Archimedes' Method

Arhimede nu cunostea functia sin, cos, tg.

By far the best demo up to now!

i just doon't know what sin and theta is but i can surely tell he explained extremely well

But 2×sin180/2=2

What about 22/7 🤔

I was able to deduce these laws without the help of anyone, I wish to be a scientist like them

oh my god i am in elementary school and this is what my teachers teach us 💀

This is not Archimedes Method.(Btw, I knew him well!)

His method did not employ trig functions at all. It only employed the Pythagorean Theorem.

You should be ashamed of yourself

Archimede is a fictional greek personality..the earliest consistent source is about 800 A.D ..THE SOURCE SUM UP DIFFERENT AUTHORS..

👏

So I made an experiment with pixel art of a circle, and I got 20/7 (close to that one number that is approximate to pi - 22/7)

      ███     
    █      █
  █          █
█              █
█              █
█              █
  █          █
    █      █
      ███     

white dots (12 + 8 = 20) / 7 (or 9 if you count the other ones, witch I think you should, but it's, umm... closer) → 20/7 or 20/9. Wait, it doesn't start with three? Oh, no!

To the fact that for the very first polygon, i.e., triangle pi comes out to be ~2.6 and for 50 sided it is 3.139 still not correct to 3 significant figures. But for a 100 sided polygon, it is 3.1410 , quite close enough.

My method is better

that doesn't have anything to do with what Archimedes did! Archimedes startet with a hexagon (aks why!) and used the thm of pythagoras to double the number of sides (ask how?) to calculate pi! he could calculate the 6- 12-, 24-, 48- and 96-gon (but not the 15-gon for instance), and he of course could not calculate sin(theta)...

too bad 180 deg is equal to pi, so the equation is lim n--> infinity (n(sin(pi/n))) = pi. kind of recursive :/

No fair using trig, as the trig functions are actually based on the value of pi.

Isnt archimedes the medic's dove? Didnt know he was also this smart

This is only half of the story as Archimedes set an upper and lower bound for the value of π. What has been discussed here is only the lower bound

prof.✍☯
considerando che 𝝿 è ,sia un angolo radiante, sia rapporto fra circonferenza e diametro sia molte altre cose le propongo due/tre soluzioni :
A)una che riguarda i cerchio trigonometrico ;
B)l'altra che deriva da una tripla Pitagorica primitiva( >7-24-25 <)
C)ed infine quella che deriva dalla tripla (3-4-5).
***************************************************************
Soluzione di A) -
180[ 1+ sen (1/N)N] dove 1/N è un numero piccolissimo che corrisponde al numero dei lati del poligono inscritto nella circonferenza. con la mia macchinetta non posso andare oltre ad N=68!
Quindi ; 180[ sen 1/68!)68!]= 180[0,017453292]=3,1415922654....=𝝿
Se lo rapportiamo al 𝚷 della macchinetta calcolatrice si ottiene 𝝿/𝚷=1,00000000....cch eè un buon risultato;
Soluzione B)
tripla→/(7-24-25)→→[( 7^3+24^3+25^3)^(1/9)] =(343+13824+15625)^(1/9)=29.792^(1/9)=
=(2^5*7^2*19)^(1/3^2)^2= 3,1413992369.. →𝝿/𝚷= - 6,37*10^(-5) (errore),
In buona sostanza si vede che 𝝿 dipende da numeri primi (2,3,5,7,19).
Soluzione C)
Tripla Pitagorica(3,4,5)
𝝿= c[b^2+c^2+2(ac)]/[8a+b)^2+(a+c)^2]→5[4^2+5^2+2(3*5)]/[(3+4)^2+(3+5)^2]
→5[(16+25+30)/(49+64)]=5(71)/113= 355/113=3,14159292...→𝝿/𝚷=1,000000085....un buonissimo risultato per i tempi di Pitagora.
Cordialità,(Joseph)
li, 28/6/23
(PS) ✍(sono persuaso che non avrò alcun riscontro ma confido che i naviganti sulla navicella di Ulisse
sappiano interpretare quando la dea Fortuna li farà naufragare su questo Sito del suo blog.)
=

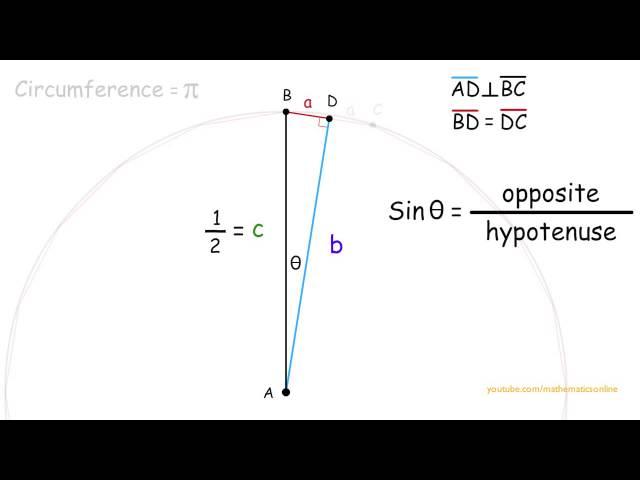
I Have A Doubt In This Question Is That You Say Sin Theta is opposite/hypotenuse i.e a/1/2 But Is Sin Theta Is Not equal To Perpendicular/hypotenuse that Will Be Equal To In This Case Will Be B/1/2

PLZ CORRECT ME

That's genius

No🔕

Newton's method takes much less work

Has anyone stopped to ask how a 360 degree circle can both start and end with a zero? How can half the diameter relative to the circumference of a predetermined set or finite set of numbers defining a Circle or sphere, be defined with an irrational number that continues forever, when the diameter and circumference are finite??

Hilarious

I actually found this on my own feeling I had an inadiquate understanding of pi so that means I’m as smart as Archimedes the only difference…

this guy did it 2300 years ago with a quill and paper no calculators no graphing calculators and literally no teaching using his own number system which most of modern society based off what a legend

Inside Outside

Fin.

It's not really Archimedes' method. He couldn't use cos/sin/tan back then. I should also mention that sin uses pi :). In doing so, you can't rely on a function to approximate pi if that function uses pi... Therefore, trigonometric functions should not be used in your demonstration.

It's not really Archimedes' method. He couldn't use cos/sin/tan back then. I should also mention that sin uses pi :). In doing so, you can't rely on a function to approximate pi if that function uses pi... Therefore, trigonometric functions should not be used in your demonstration.

It's not really Archimedes' method. He couldn't use cos/sin/tan back then. I should also mention that sin uses pi :). In doing so, you can't rely on a function to approximate pi if that function uses pi... Therefore, trigonometric functions should not be used in your demonstration.

By that logic calculating pi precisely be equivalent to dividing by 0 or a divergent infinite sum. That makes more more intuitive sense of euler’s infinite series calculations ending up with pi

I am very surprised to see that the formula i derived for pi four days ago independently was already derive by Archimedes .😅

n=1, 1sin(180°÷1)not equal to pi value
Any have a condition for n?

Archimedes also used the EXTERIOR polygons to establish the RANGE of the true value of PI. Not just the inscribed polygons.

I’m year 5 and I understand this

This is not what Archimedes did.
You just replaced a problem with another problem computing Pi by computing sinus.
Check a video of MathWithoutBorders he explained how he did

Try this: The cord length of 1/60° (minute of angle) included angle in inches. At exactly 300 yards (10800) inches. sin 1/120° x 10800 x 2 = PI.....My calculator rounds to 9 digits, excel can round to 100 digits.

thank you, I love you my friend <3

bruh i am just year 9 and i work out this just when I learnt trigonometry, but I used x*tan(180/x) instead of x*sin(180/x) is it actually that hard to work out this?

But this is cheating; the tabulation of the sin function depends on knowing pi. So it doesn't Calculate pi from first principles.

Excellent explanation

Yeah but I want to know how Archimedes calculated Pi using only a stick with which to draw in the dirt.

It expands outwards

(180/x)*(sin(x)/cos(0.5x)) , x has to be in degrees and the closer you get it to 0, the better you get it. Oh, and you can't simplify it using identities because it won't work then (I think). I think its takes away a solution or something. But yeah, this works.

You forgot to credit Archimedes. For using this method.

This is a circular argument, as one needs to know the value of pi to compute sin(180º/n). This is because sin(180º/n) = sin(pi/n), and any value of sin(x) must be computed with a series (or by direct measure drawing a big circle). So, as n goes to infinity, sin(pi/n) goes to pi/n, and n*pi/n = pi. Yes, I know that this is a introductory video to the topic, but I found important to comunicate this.

Thank you for clear and easy explanation, I look for on many channels but your is the best. Really deserves like and subscribe.

If you take the limit as n tends to infinity you get 180 😢

This is recursive though…

n(sin(pi/n))